Performance Summary

This summary showcases the significant computational performance of the gwsnr package compared to traditional methods like those in bilby. We benchmark two main computational techniques: the high-accuracy inner-product (or noise weighted inner-product) method and the ultra-fast interpolation (or partial-scaling interpolation) method.

Test Environment

Our benchmarks were run using two main configurations:

• Config-1: Performance benchmarks conducted using a fixed set of 100,000 astrophysically motivated waveform parameters for both Binary Black Hole (BBH) and Binary Neutron Star (BNS) systems, generated with the ler software package. BNS waveforms are significantly longer in duration than BBH waveforms, highlighting the performance benefits of gwsnr for extended-duration gravitational wave signals. Performance is benchmarked against bilby’s traditional optimal SNR computation method.

• Config-2: Scaling analysis using randomly sampled BBH events in 10 batches, ranging from 10,000 to 100,000 events for the inner-product method and up to 1,000,000 events for the interpolation method. All parameters are sampled using the same methodology as Config-1 to demonstrate how performance scales with increasing computational workloads, in a realistic astrophysical context.

Inner-Product Performance

Benchmark Results (100,000 Events)

The noise weighted inner-product is the foundation of the SNR calculation. gwsnr’s multi-core CPU architecture significantly reduces computation time compared to bilby’s single-core approach. gwsnr inner-product has optimization and utilizes numba.njit for just-in-time compilation of computationally intensive functions, including signal duration calculations, antenna response computations, and the inner-product calculation itself. The table below summarizes the performance comparison:

Hardware Acceleration	Machine Specification	Time [s] (BBH, BNS)	Speedup vs. bilby’s Inner-Product
gwsnr (multi-core)	Apple M2 Pro, 4 CPU cores	16.652, 122.879	4x, 4.8x
bilby (single-core)	Apple M2 Pro, 1 CPU core	65.871, 443.625	1x, 1x

Multi-core parallelization in gwsnr provides a significant advantage. While the speedup for the shorter BBH signal is evidently ~4x, from the use of 4 CPU cores, the performance gain for the long BNS waveform is over 4x. It makes gwsnr an ideal choice for modest computation duration with high SNR accuracy.

Performance Scaling

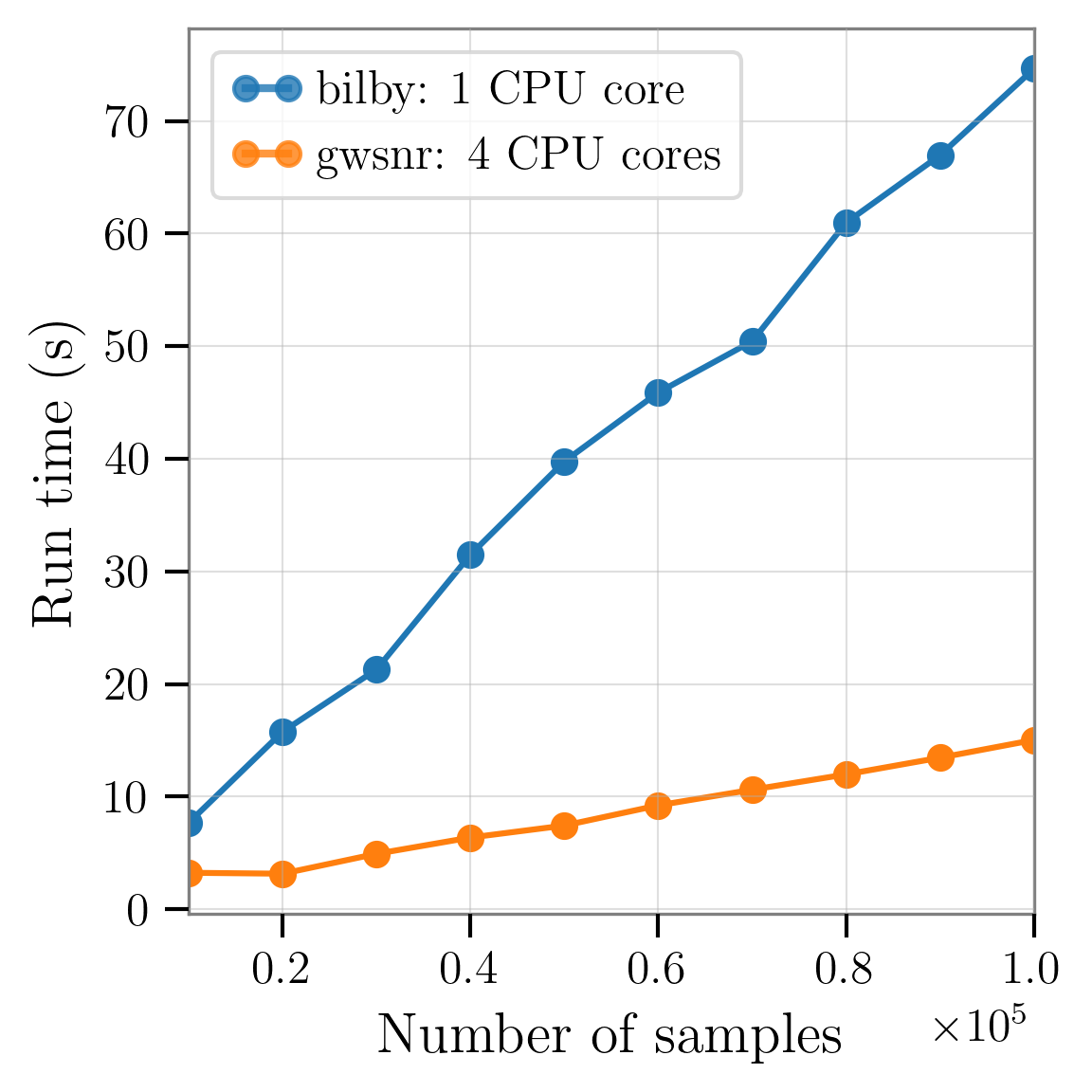
Figure 1: This plot compares the computational speed of the gwsnr package's inner-product implementation against the traditional SNR computation using bilby. The plot shows the run time (in seconds) required to evaluate an increasing number of parameter samples from 10000 to 100,000 BBH samples. The bilby benchmark was run on a single CPU core. In contrast, gwsnr leverages both multi-core processing (using four cores in this test) and just-in-time (JIT) compilation with numba to accelerate intensive calculations. The performance of gwsnr is also scalable and would improve further with additional CPU cores. The results clearly show that gwsnr is significantly more efficient, and its performance advantage grows with the number of samples. Importantly, this speedup is achieved without compromising accuracy, as both methods yield identical SNR values.

As shown in Figure 1, gwsnr’s multi-core efficiency provides a sustained advantage that grows with the size of the dataset, making it significantly more scalable than single-core implementations.

Interpolation Performance

Benchmark Results (100,000 Events)

Large-scale SNR calculations requiring millisecond-level computation are achieved through gwsnr’s interpolation technique, which bypasses the need to generate full GW waveforms for SNR calculation. This computationally lightweight interpolation method enables just-in-time compilation and massive parallelization across multi-threaded CPU and GPU architectures, delivering exceptional performance improvements, particularly for extended-duration signals such as BNS systems. A key advantage of the interpolation method is that computation time scales with the number of interpolation points rather than waveform duration, providing consistent performance regardless of signal length. The table below summarizes the performance benchmarks for different hardware configurations with gwsnr interpolation method for SNR calculations:

Hardware Acceleration	Machine Specification	Time [ms] (BBH, BNS)	Speedup vs. bilby’s Inner-Product
GPU (jax)	NVIDIA RTX 3080, GPU	79	834x, 5616x
GPU (mlx)	Apple M2 Pro, GPU	94	700x, 4719x
CPU (jax)	Apple M2 Pro, 10-core CPU	187	352x, 2372x
CPU (numba)	Apple M2 Pro, 10-core CPU	193	341x, 2298x

The GPU acceleration with jax (or mlx) achieve remarkable speedups of over 5000x (or 4000x) compared to the bilby baseline, especially beneficial for longer BNS waveforms. Even CPU-based implementations using JAX and Numba demonstrate speedups of several thousand times, highlighting the method’s exceptional efficiency across different hardware configurations.

Practical Impact: In the ler package, gwsnr is used for SNR computation of sampled events (e.g., BNS) in batches of 100,000 to 1 million events to determine detection rates based on SNR thresholds. The cumulative speedup can save more than 1 hour 13 minutes 55.46 seconds of computation time compared to traditional methods.

Performance Scaling

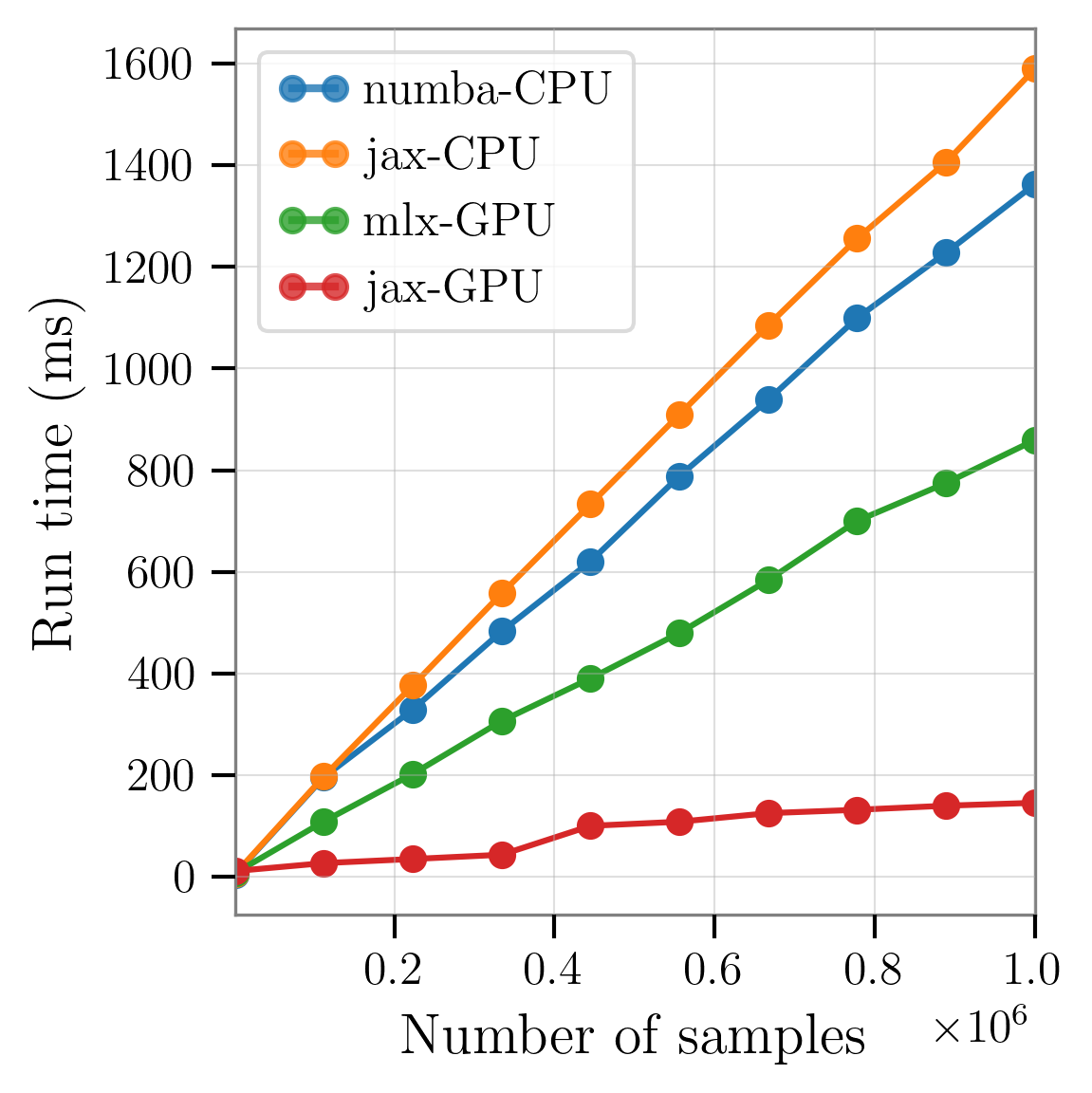
Figure. This plot compares among the interpolation methods, that uses different hardware accelerations, available in gwsnr. The plot shows the run time (in ms) required to evaluate an increasing number of parameter samples from 1000 to 1000,000 samples. Performance is maximized with GPU acceleration, particularly for larger sample sizes. This comes from the massive parallelism offered by GPUs, much more the than the multi-threaded CPU implementations.

The interpolation performance analysis highlights the significant advantages of the gwsnr package in terms of computational efficiency especially when sample size increases. The results demonstrate that GPU acceleration, particularly with the jax backend, can achieve speedups nearly 10x compared to its CPU counterparts.

Conclusion

The gwsnr package offers a compelling performance advantage for gravitational-wave SNR calculations. The results clearly show massive speedups with gwsnr’s interpolation and notable speedups with inner-product calculations with multi-processing, especially for long-duration signals. This makes gwsnr a powerful tool for accelerating a wide range of gravitational-wave simulation and data analysis tasks.